Calculating vectors will be a piece of cake from now on. Calculate3D calculates all the mathematical problems which arise in vector analysis and shows you the entire solution route, together with brief annotations (not in lite version).
Because of that Calculate3D is the ideal companion for your final examination preparations and all your homework concerning vector analysis.
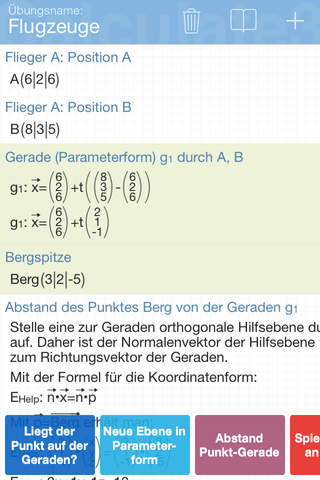
You want to calculate the distance of a point to a plane or the point where to straights intersect? Calculate3D is the answer to your pains. Your homework will be done in the blink of an eye.
Calculate3D serves all students in the final stage of secondary school as well as college students who work on analytical geometry.
Calculate3D helps you to improve your skills in the field of analytical geometry as well as vector analysis with brief annotations and by showing you the solution route step by step (not in lite version). It simplifies the work on vectors and makes a pocket calculator neglectable.
In addition to all the perks of this apps there are neither any in-app purchases nor any costs for internet connection because the app doesnt require an internet connection.
App features
• Calculate3D can perform all calculations of vector analysis
• the entire solution route is shown and accompanied by brief annotations (not in lite version)
• the handling is absolutely intuitiv and easy to understand
• experienced users can deactivate all helps in the calculation process
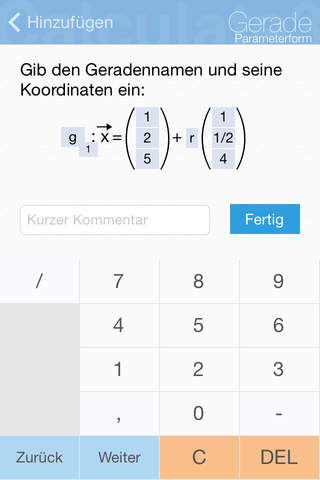
• easy input of variables, points, vectors, planes, matrices without any complicated commands
• extensive mathematical annotations
• annotations and solution routes can be deactivated
• saves all calculations automatically
• similar exercises can be calculated rather quick because the variables can be altered at any time
Mathematical content
• 3D objects: points, vectors, lines, planes
• Trackpoints of lines and planes
• Reflections
• Dot (scalar) product and vector product (cross product) and matrix product
• Converting the form of a planes (parametric form, coordinate
form and normal form)
• Angle calculations
• Linear dependence of vectors (collinear and complanar vectors)
• Positional relationships of points, lines and planes
• Intersection points of lines and planes
• Line of intersection of two planes
• Distance calculations of points, lines and planes
• Matrix operations (sums, differences, products, determinants ...)
• projection matrices on coordinate planes or other planes