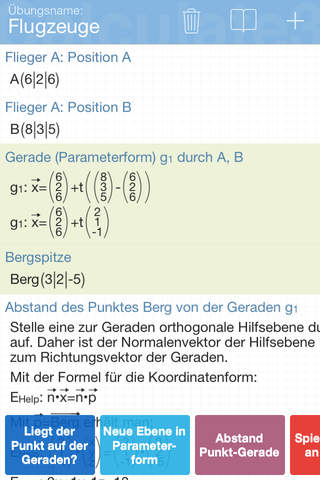
Calculate3D löst für dich alle Probleme, die in der Vektorrechnung auftreten und zeigt dir den kompletten Lösungsweg (nicht in der Lite-Version) mit kurzen Erläuterungen.
Ab jetzt werden die Hausaufgaben der Vektorrechnung zu einem netten und kurzem Zeitvertreib.
Calculate3D ist für alle Schüler der gymnasialen Oberstufe und für alle Studenten geeignet, deren Mathematikthema die analytische Geometrie ist. Calculate3D hilft dir die Vektorrechnung mit intelligenten Vorschlägen besser zu verstehen und zeigt Schritt für Schritt den Lösungsweg (nicht in der Lite-Version). Calculate3D nimmt dir viele Arbeitsschritte ab und macht den Taschenrechner annähernd überflüssig.
Außerdem fallen keine weiteren Kosten durch InApp-Käufe oder Internetgebühren an, denn Calculate3D benötigt keine Internetverbindung.
Leistungen der App
• Calculate3D beherrscht alle wichtigen Berechnungen zu Problemen, die im Mathematikunterricht in der Schule auftreten
• Der komplette Lösungsweg wird angezeigt und erläutert (nicht in der Lite-Version)
• Die Bedienung ist intuitiv und sehr leicht zu verstehen
• Für erfahrene Nutzer können Hilfen, die die Bedienung erleichtern, deaktiviert werden
• Einfache Eingabe von Variablen, Punkten, Vektoren, Ebenen und Matrizen ohne komplizierte Befehle
• Umfangreiche mathematische Erläuterungen
• Erläuterungen und Rechenwege können ein- und ausgeblendet werden
• Speichert automatisch alle Übungen
• Viele gleichartige Aufgaben lassen sich schnell berechnen, da die Variablenwerte jederzeit geändert werden können
Mathematische Inhalte
• 3D Objekte: Punkte, Vektoren, Geraden, Ebenen
• Spurpunkte von Geraden
• Achsenabschnittspunkte von Ebenen
• Spiegelungen
• Skalarprodukt und Vektorprodukt (Kreuzprodukt), sowie Matrizenprodukt
• Umwandeln von Ebenendarstellungen (Parameterform, Koordinatenform und Normalenform)
• Winkelberechnungen
• Lineare Abhängigkeit von Vektoren (kollineare und komplanare Vektoren)
• Lagebeziehungen von Punkten, Geraden und Ebenen
• Schnittpunkte von Geraden und Ebenen
• Schnittgeraden von zwei Ebenen
• Abstandsberechnungen von Punkten, Geraden und Ebenen
• Matrizenoperationen (Summen, Differenzen, Produkte, Determinanten...)
• Projektionsmatrizen auf Koordinatenebenen oder auf beliebige Ebenen